用正则表达式判断一个二进制数能否被3整除
问题描述如标题,很简洁:用一个正则表达式判断一个二进制数能否被3整除
比如:
000 True
11 True
1001 True
1011 False
解决思路也很简单:首先用有限状态机(FSM)实现对能否被3整除的判断,然后将其转换成正则
有限状态机图如下,分析过程摘自matrix67,并在此感谢一下神犇
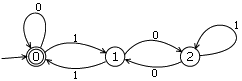
注意到,一个二进制数后面加一个“0”相当于该数乘以2,一个二进制数后面加一个“1”相当于该数乘2加1。设定三个状态,分别叫做0、1和2,它们表示当前的数除以3所得的余数。如果对于某个i和j,有i*2≡j (mod 3),就加一条路径i→j,路径上标一个字符“0”;如果i*2+1≡j (mod 3),则在路径i→j上标记“1”。状态0既是我们的初始状态,也是我们的最终状态。我们的自动机就做好了。现在,假如二进制数10010走进来了。从状态0出发,机器首先读到一个“1”,于是当前位置挪到状态1,表明目前该数模3余1;然后,系统读了一个“0”,我们紧跟着走到状态2,表明二进制数“10”被3除余2;下一步,我们回到状态1,表明“100”除以3余1;再往后,我们得知“1001”能被3整除。最后呢,我们读到一个0,“1001”的两倍当然还是能被3整除,我们依旧停留在原位。我们得到结论:二进制数10010能被3整除。
有限状态自动机是可以转化为正则表达式的。上面的这个自动机转化起来非常容易。我们可以先试着用自然语言叙述一下。首先,每个二进制数第一位必然为“1”。到达状态1后,我们可以随意地、任意多次地在状态1周围绕圈圈,最终回到状态1。临近末尾,我们再读到一个“1”返回状态0,这之后随便读多少个“0”都可以了。现在问题分解为:我们又如何用正则表达式表述“从状态1出发随意地走最终回到状态1”呢?在本例中,这是很好描述的:它可以是字符串“1000..001”和“0111..110”的任意组合。把这些东西用正则表达式写出来,就是我们刚才那个神秘的式子:1((10*1)|(01*0))*10* 。
最后再加上位置标识符,^1((10*1)|(01*0))*10*$
从matrix67的分析自然语言可以理解正则,但是从有限状态机转换到正则的通式通法还不会。